GRRR BAW ici Boris, et aujourd’hui on va parler CÉ-FRAN. Oui ça fait des mois qu’on vous gave avec les élections, mais calmez-vous, ça va bien se passer il ne sera ici question que d’un peu de sciences et d’informatique. Désolé pour le retard, l’article était censé être publié pendant l’entre-deux tours, puis a été repoussé aux législatives, puis à maintenant… mais les croisés tu connais.
DISCLAIMER : Aucune notion d’informatique n’est nécessaire à la compréhension de l’article, il vous suffit donc d’ignorer les solutions en Go si ces dernières ne vous intéressent pas.
Un peu de théorie du choix social…
Hein, c’est un blog de tech ou de socio ?! Pas si vite, on va voir que les deux thématiques peuvent être beaucoup plus proches qu’on ne le pense, et que mêler politique et choix computationnel n’est finalement pas si aberrant.
On peut définir la théorie du choix social comme l’étude du processus menant les préférences individuelles à la préférence collective d’une société. Cette préférence peut être un classement des choix possibles (appelé fonction de bien-être social) ou une décision unique (appelée fonction de choix social). Attention voyageur fortuit !!! Posons les bases : les votants seront supposés tous égaux et présenteront leur choix sous forme d’ordre total. Si vos cours de maternelle semblent trop lointains, retenez que les ordres totaux permettent de toujours discriminer deux éléments.
17
Comme le nombre de titres des Boston Celtics, ou encore le nombre de systèmes électoraux existants à travers le monde. Oui, ça en fait un paquet, et oui gaulois, il n’y a pas que le scrutin uninominal majoritaire à deux tours ! Mais que mène un État à choisir un mode de scrutin plutôt qu’un autre ? Comment faire pour séparer les bonnes fonctions de choix social des moins bonnes ? C’est ici qu’on va faire appel à la Dream Team des bonnes propriétés :
- Universalité : l’élection doit toujours aboutir à un résultat, peu importe les candidats et votants
- Unanimité : si tous les votants préfèrent Jonathan Cohen à Emmanuel Macron, alors Jonathan Cohen doit devenir Président de la République
- IAND (Indépendance des Alternatives Non-Disponibles) : si les votants préfèrent un candidat à un autre, alors l’entrée d’un nouveau candidat dans la course ne devrait pas altérer cette préférence (ce qui est en principe assez difficile à vérifier)
- Absence de Dictateur : la règle de choix social n’obéit à aucun individuIl suffit donc de trouver la méthode capable de satisfaire cet ensemble non ? Pas si vite, car selon le théorème d’impossibilité d’Arrow (1951), aucune fonction de choix social n’est en mesure de satisfaire simultanément toutes ces propriétés cries in democrat.
Désolé de briser vos rêves, mais devons-nous pour autant en conclure que la démocratie n’est qu’une utopie ? Bof, et l’une des méthodes pour contourner ce théorème pourrait être de pondérer l’importance de chaque propriété dans la construction d’une démocratie : respecter la dernière propriété (Absence de Dictateur) serait par exemple une condition sine qua non, et si vous n’êtes pas d’accord qu’est-ce que vous foutez à lire un article pareil ??
Comme chez Coddity on n’enfile pas des Perl, cette petite étude sera servie sur son lit d’implémentations en Go, histoire de rendre tout cela (un peu) sophistiqué et faire semblant de faire du choix social computationnel.
On va donc se munir des structures suivantes, qui nous seront utiles pour toutes les méthodes de vote :
type Candidate struct {
Id int
Name string
}
type Voter struct {
Id int
Name string
Vote ScrutinIndiv
}
type Result struct {
DuelsWon int
TotalPoints int
WonAgainst []Candidate
}
type ResultPerCandidate struct {
Cand Candidate
Res Result
}
type Pair struct {
L Candidate
R Candidate
}
type ScrutinIndiv []CandidateAinsi, quels sont les avantages et inconvénients des différentes méthodes ? Est-il possible de les comparer ? Pourquoi notre système actuel n'est-il pas optimal ? Ce sont les questions auxquelles nous allons tenter de répondre dans cet article.
Allez, on respire… c’est parti !
Le scrutin uninominal majoritaire à deux tours 🇫🇷
Cette méthode est naturelle pour nous, et certains peuvent voir d’un œil étranger les pays où les élections se déroulent différemment. Elle a certes l’avantage d’être facile à mettre en place, permet un dépouillement très rapide, mais ce chauvinisme est-il justifié ? Spoiler alert : elle présente en réalité de nombreux défauts, le premier étant la manipulabilité, où il peut être profitable à un électeur de mentir sur ses préférences. Supposons que pour les candidats A, B, C, D on ait :
- 20 votants ayant la préférence C > A > D > B
- 12 votants ayant B > A > C > D
- 10 votants ayant A > D > B > CEn l’état, C serait élu. Cependant, si les 12 votants préférant B forment une coalition et décident de voter ensemble pour A, alors ce dernier serait élu, malgré le fait qu’ils préfèrent B. Manipulabilité vous avez dit ?
De plus, elle permet la dictature de la majorité au travers du vote utile, n’incitant donc pas vraiment à la participation ("Que je vote ou pas, ça ne changera rien"). Par conséquent, ceci favorise une division bipartite du paysage politique, désavantageant par la même occasion les candidats les moins influents. Enfin, il n’est ici pas possible de vérifier l’IAND, puisqu’au premier tour, on risque d’éliminer un candidat pourtant préféré aux autres (voir critère de Condorcet plus bas).
Lorsqu’on voit que l’abstention concerne 1⁄4 des inscrits, on peut se demander si l’élection désigne réellement le candidat que les Français souhaitent en majorité. Bref, arrêtons le massacre, et passons à l’implémentation pour y voir un peu plus clair (ou pas) :
func TwoRoundSystem(voters []model.Voter, c []model.Candidate) model.ResultList {
count := make(map[model.Candidate]int)
secondRoundList := make([]model.Candidate, 0)
// Appel à une fonction de service qui va simuler le scrutin
// en suivant ses règles
firstRoundResult := majorityProcedure(voters, c, count)
if len(firstRoundResult) == 1 {
return firstRoundResult
} else {
for i := range firstRoundResult {
secondRoundList = append(secondRoundList, firstRoundResult[i].Cand)
// Appel recursif avec les candidats qualifiés au
// second tour
finalRes := TwoRoundSystem(voters, secondRoundList)
return finalRes
}
}
return model.ResultList{}
}
func majorityProcedure(voters []model.Voter, candidates []model.Candidate, res map[model.Candidate]int) model.ResultList {
resultList := make(model.ResultList, len(res))
resPair := make(model.ResultList, 0)
total := 0
for _, v := range voters {
for i, alternative := range candidates {
// On parcourt les choix de chaque votant
if v.Vote.IndexOf(candidates[i]) == alternative.Id {
res[alternative] += 1
total++
}
}
}
for k, v := range res {
// On affecte à chaque candidat le nombre de voix récoltées
resultList = append(resultList, model.ResultPerCandidate{
Cand: k,
Res: model.Result{
TotalPoints: v,
},
})
}
sort.Sort(sort.Reverse(resultList))
// Ballot est une fonction dont le comportement dépend de la méthode
// choisie (implémentation détaillée sur le repository GitHub)
resPair, shouldReturn, returnValue := model.Ballot("majority", resultList, total, resPair, candidates)
if shouldReturn {
return returnValue
}
return resPair
}Le vote par approbation
Ce scrutin en deux tours est assez particulier, car permet aux électeurs de voter pour plusieurs candidats au premier tour, ce qui règle le problème de dispersion des votes. Mais encore une fois, le vote stratégique reste possible, puisqu’on est naturellement tenté de ne pas voter pour un candidat pouvant potentiellement battre notre champion. De plus, il n'y a pas d'échelle de valeurs entre les votes : un vote en faveur d'un candidat populaire et un vote pour un candidat dont la victoire est peu crédible serait traité de la même façon (ce qui peut être aussi bien positif que négatif, selon le point de vue).
En 2002, une expérience[1] a été menée sur 5 bureaux de vote à Orsay, avec un échantillon de 2597 votants. Voici le nombre d’assentiments (nombre de candidats qu’un électeur choisit) par bulletin :

Voyons les résultats à partir de jolis graphiques :
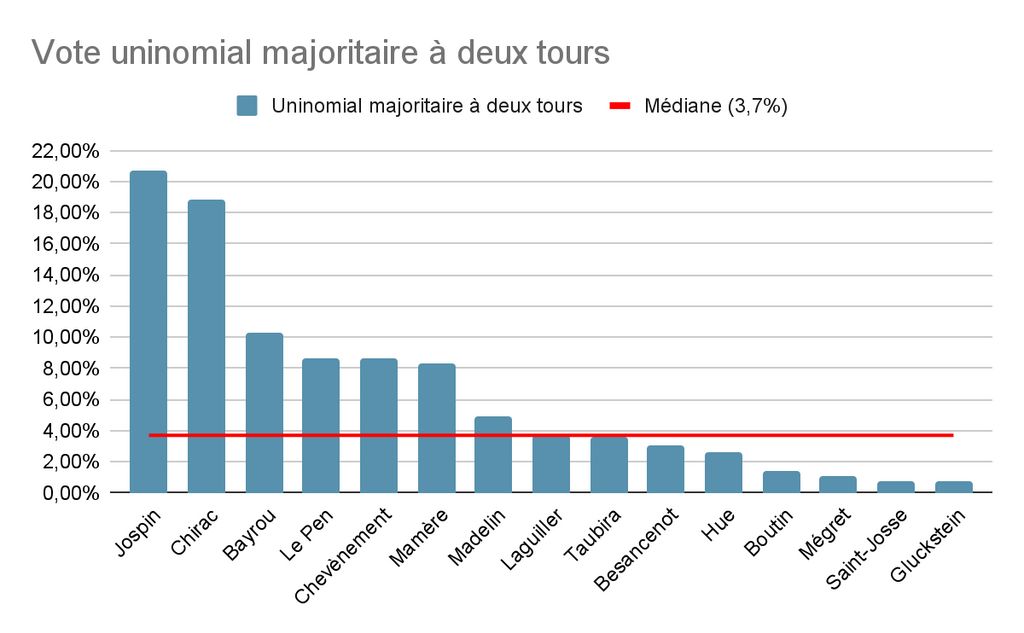
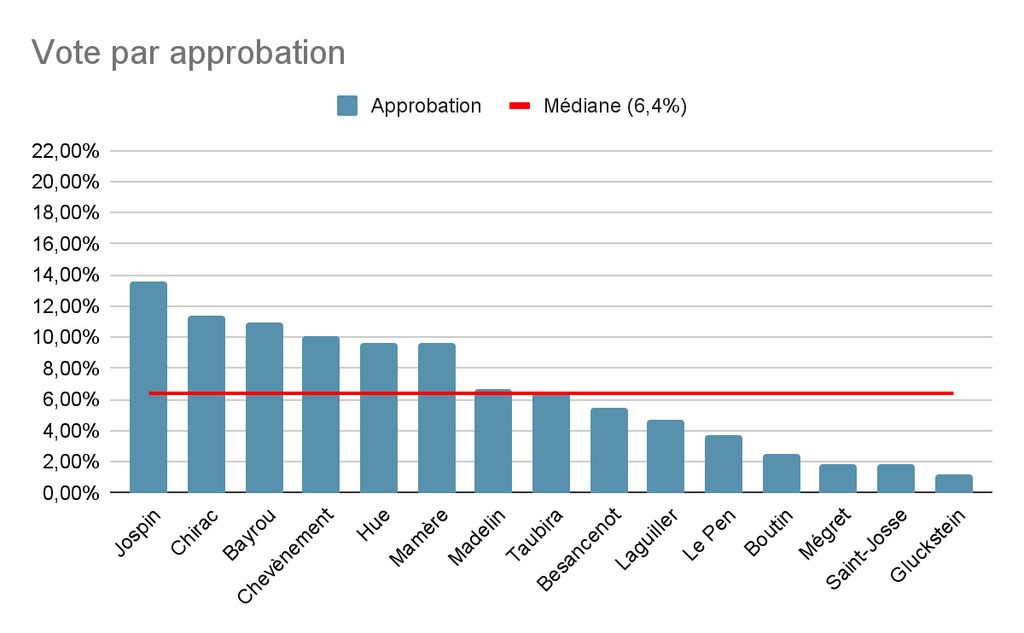
Oui les candidats passant au deuxième tour sont les mêmes. Cependant, on observe que le vote par approbation apporte un résultat plus serré, avec une qualification au second tour beaucoup moins confortable pour Lionel Jospin et Jacques Chirac. On a par exemple Noël Mamère qui se trouve à seulement 1,8% du second tour, malgré sa sixième place. De plus, si l’on compare les médianes des deux scrutins (pour flex : test statistique de Mood), on peut parvenir à la conclusion que l’assentiment permet une meilleure distribution des votes, et donc une meilleure considération des souhaits des électeurs.
Voyons ce que ça donne en Go :
// La différence avec le vote majoritaire réside ici, dans la fonction Ballot
func Ballot(votingMethod string, resultList ResultList, total int, resPair ResultList, candidates []Candidate) (ResultList, bool, ResultList) {
for cand := range resultList {
percentage := (resultList[cand].Res.TotalPoints * 100) / total
if percentage > 50 {
resPair = append(resPair, ResultPerCandidate{
Cand: resultList[0].Cand,
Res: Result{
TotalPoints: resultList[0].Res.TotalPoints,
},
})
return nil, true, resPair
} else {
for i := 0; i < len(candidates)-1; i++ {
// Disjonction de cas entre l’approbation et le vote majoritaire
if votingMethod == "approval" {
resPair = append(resPair, resultList[i])
} else if votingMethod == "majority" {
resPair = append(resPair, resultList[0], resultList[1])
}
return nil, true, resPair
}
}
}
return resPair, false, nil
}La méthode de Condorcet
Remontons à 1785, où fut défini le vainqueur de Condorcet. On peut le définir comme le candidat préféré à tous les autres, pris un par un. Autrement dit, c’est comme si on avait pleins de tournois en cage 1v1 entre tous les candidats, et s’il existe un candidat mettant KO tous les autres pendant la majorité des combats, alors c’est le vainqueur de Condorcet.
On pourrait illustrer cela à l’aide d’un graphe de majorité non-transitif, où un arc reliant le candidat A au candidat B signifie qu’une majorité stricte de votants préfèrent A à B : el ganador de Condorceto serait donc le candidat pointant vers tous les nœuds.
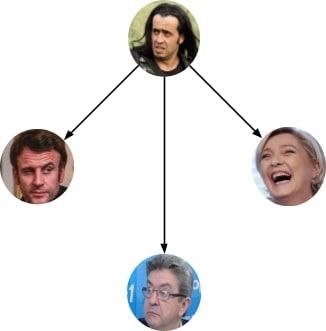
Cette méthode paraît très séduisante, puisqu’elle annihile la notion de vote utile et donc supprime les inégalités entre "petits" et "grands" candidats : pratique ! Pour l’anecdote, Nicolas Sarkozy fut élu président de la République à l’issue de l’élection de 2007, tandis que les sondages indiquaient une préférence des Français pour François Bayrou par rapport à Sarkozy (et à chaque autre candidat) wtf la démocractie ???
Pauvre François, validé par les Français mais même pas foutu de se qualifier au second tour…
GoGoGo :
func CondorcetVoteRound(votes []model.Voter, candidates []model.Candidate) (model.Candidate, model.Result) {
now := time.Now()
possiblePairDiff, resultList := model.GeneratePossiblePairDiffsAndResultList(candidates)
// On récupère le score de chaque duel pour chacun des votants
fmt.Println("---- before setPossiblePairDiffValue", time.Since(now))
model.SetPossiblePairDiffValue(possiblePairDiff, votes)
fmt.Println("--- after setPossiblePairDiffValue", time.Since(now))
now = time.Now()
// Liste des résultats
model.SetResultListValue(possiblePairDiff, resultList)
now = time.Now()
// On récupère un gagnant
var result model.Result = model.Result{}
var candidat model.Candidate = model.Candidate{}
for r, v := range resultList {
if result.DuelsWon < v.DuelsWon {
result = *v
candidat = r
}
}
return candidat, result
}Cependant, ce système peut être victime d’un phénomène assez embêtant : le paradoxe de Condorcet. Tah un Pierre-Feuille-Ciseau où A serait préféré à B, B à C, et C à A. Pour y remédier, une règle de tie-break doit être définie afin de déterminer le gagnant selon une loi de probabilité. Mais c’est relou à faire, puis allez expliquer à René 85 ans ou Mathilde 15 ans que non, ça ne signifie pas que le président va être tiré au sort.
Ainsi, pour s’affranchir de cette peine, des pays comme l’Australie ou l’Irlande ont adopté une méthode dérivée, où chaque électeur classe les candidats par ordre de préférence : le vote alternatif.
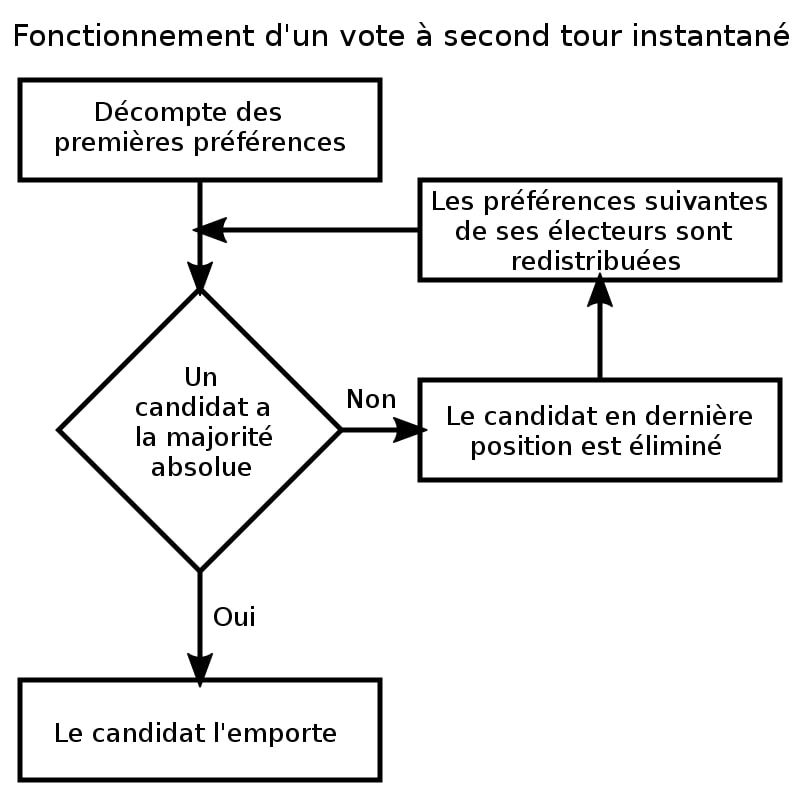
On ne rentrera pas plus en détail de cette méthode dérivée de Condorcet, mais la chose à retenir est que l'obligation d’obtenir une majorité absolue augmente fortement la légitimité de l’élu, mais ne permet pas toutefois d’élir forcément un gagnant de Condorcet, dommage... Heureusement, il existe un moyen d’y remédier.
La méthode de Copeland
Cet article peut donner l’impression que l’on se dirige petit-à-petit vers la quintessence de la démocratie, mais rappelez-vous d’une chose : il n’existe pas de méthode de vote parfaite, juste des moins pires que d’autres. L’objectif est de maximiser le nombre d’électeurs dont le vote suivrait strictement leurs préférences, et en ce sens, la règle de Copeland ne paraît pas trop déconnante.
En bref, Copeland est un mix de Condorcet et du vote alternatif, modulo les défauts, ce qui signifie qu’à la fin d’une procédure de Copeland, on est censé avoir élu un vainqueur de Condorcet. Notons que cette méthode de vote reste sujette aux manipulations, où l’on peut voir apparaître par exemple des coalitions pour nuire à un adversaire. Mais dans cet article nous vivons dans un monde idéal , alors pas de risque à ce niveau-là.
Concrètement, pour le candidat i, on va établir une matrice antisymétrique de taille n×n (avec n ≥ 2 le nombre de candidats), construite telle qu’une cellule vaut :
- (+1) si i est strictement préféré au candidat j pour l’ensemble des électeurs
- (-1) si j est strictement préféré à iOn définit alors le score de Copeland de i comme la somme sur j des cellules concernées. Si le candidat i obtient un score de n - 1, jackpot : il est alors vainqueur de Copeland ET de Condorcet. Rien que ça.
Voyons un exemple très simple, avec la combinaison de préférences individuelles ci-dessous pour les candidats A, B, C et D obtenues après dépouillement :
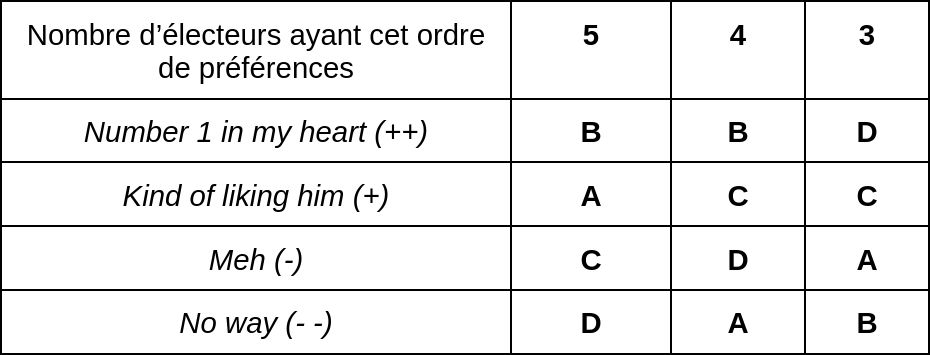
On obtient alors la matrice suivante :
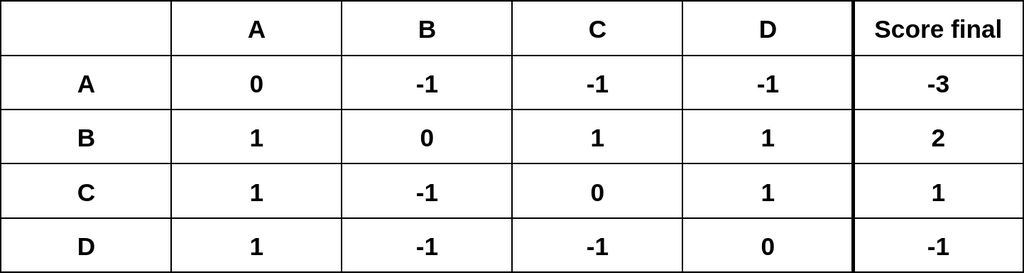
Ainsi, B est élu puisqu’il est l’unique candidat capable de satisfaire le critère de Condorcet, ce qu’on peut illustrer encore une fois par le graphe complet suivant :
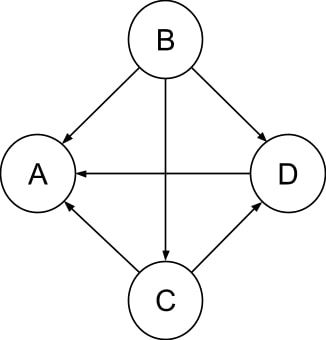
Place à l’implémentation en Go, pour notre plus grand plaisir (ou détresse) :
// Petit tricks : Calculer le score de Copeland à partir d’un vote
// de Condorcet pour s’affranchir de la manipulation matricielle
func Copeland(voters []model.Voter, candidates []model.Candidate) (model.Candidate, int) {
numberOfDuels := len(candidates) - 1
candidat, result := CondorcetVoteRound(voters, candidates)
duelLost := numberOfDuels - result.DuelsWon
// result.DuelsWon - duelLost correspond au score de Copeland
return candidat, result.DuelsWon - duelLost
}Vers un changement du mode de scrutin en France ?
Alors finalement, le changement c’est maintenant ? Dans les faits, très peu. Les considérations politiques[2] représentent d’importants obstacles à une éventuelle évolution, et plus le temps passe, plus les perspectives de changement s’éloignent au vu du conservatisme dont fait preuve le droit électoral français[3].
Cependant, on observe sur les réseaux sociaux de plus en plus de personnes pointant du doigt notre système actuel, avec un vote utile ayant été plus que jamais au cœur des débats. Plus que de simples articles hypothétiques de revues, de vrais travaux sont en cours, initiés par une expérience menée en 2017 par des chercheurs du CNRS, en partenariat avec l’Université de Paris-Dauphine et l’Ecole Polytechnique. L’objet de leur étude fut de voir quel serait le résultat du scrutin présidentiel de 2017 en procédant au Jugement Majoritaire, méthode étudiée par ailleurs par l’un de nos lauréats de la bourse Coddity en 2017 ! Ils ont pu mettre en place cette méthode à partir d’un échantillon de 52 000 personnes, et bien que les résultats ne soient pas parfaits, il est bon de voir que certains s’emploient à étudier les alternatives pouvant être réellement mises en place ! Vous pourrez trouver toutes les infos la concernant sur leur site.
J’espère que cet article vous a plu, et si vous souhaitez voir en détail l’implémentation vous trouverez tout sur ce repo GitHub. (n’hésitez pas à ajouter une petite star la famille ça fait toujours plaisir)
NB : N’étant que stagiaire, je remercie Charles pour la code review et le super mocks generator, et me dédouane donc de toute responsabilité vis-à-vis d’éventuelles non-optimalités.
A BIENTOT LA MIF
Sources :
[1] Jean-François Laslier, Karine van der Straeten. Élection présidentielle : Une expérience pour un autre mode de scrutin. 2003. hal-00242952
[2] Quinault-Maupoil, T. (2021, 2 mars). Proportionnelle : l’option parlementaire se corse. Le Figaro. https://www.lefigaro.fr/politique/proportionnelle-l-option-parlementaire-se-corse-20210302
[3] Rambaud, A. R. (2021, 4 mars). Est-il encore possible de changer les règles des élections de 2022 ? Blog du droit électoral. https://blogdudroitelectoral.fr/2021/03/est-il-encore-possible-de-changer-les-regles-des-elections-de-2022-r-rambaud/




